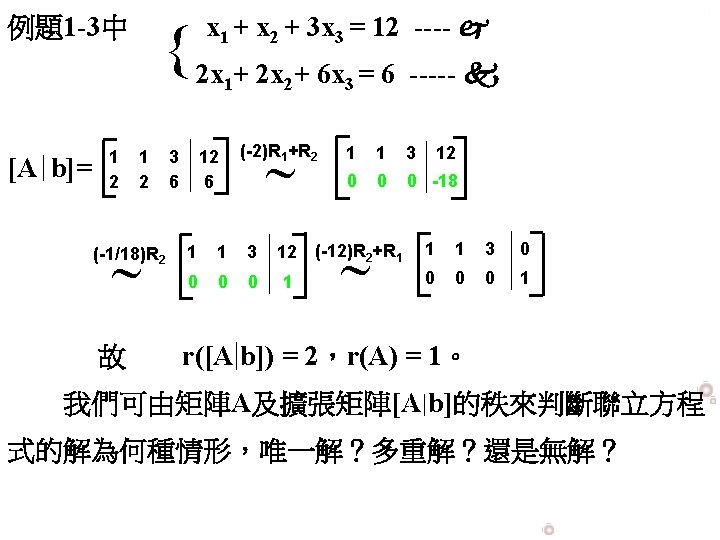
21 連立一次方程式と行列 連立一次方程式とは ;例題5 以下の連立方程式が解を持つように,aを定めて解を求めよ. x y z= 6 x y 2z= 11 2x 2y− 4z= a (解答) 1 1 1 6 1 1 2 11 2 2 −4 a → 1 1 1 6 0 0 1 5 0 0 −6 a−12 → 1 1 0 1 0 0 1 5 0 0 0 a18 よって連立1次方程式は x y z= 6 z= 5 0= a18 と変形された 最後の式に注目すると,a18=0第3回 方程式の代数化と連立一次方程式の解法 筑波大学システム情報工学科 構造エネルギー工学専攻 田中聖三 基礎方程式の離散化 => 連立1次方程式(flow) Q数値解析とは? A 基礎方程式を離散化して最終的に得られる連立1次方程式を解く. 基礎方程式(1次元Laplace方程式) 差分方程式の代数

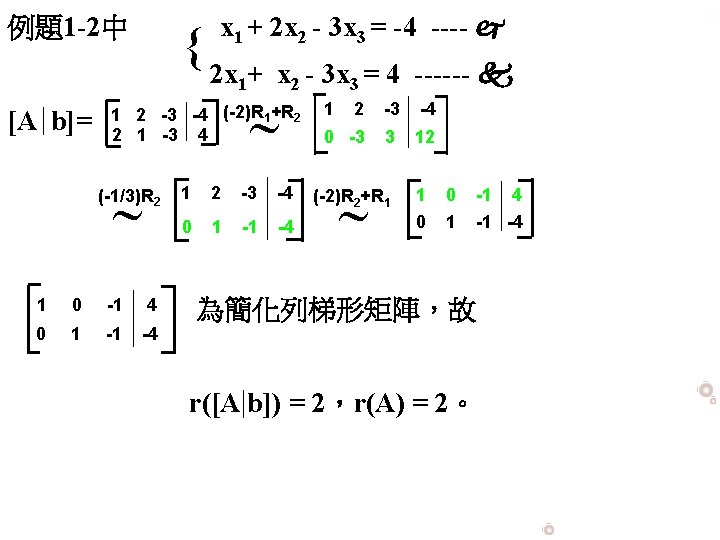
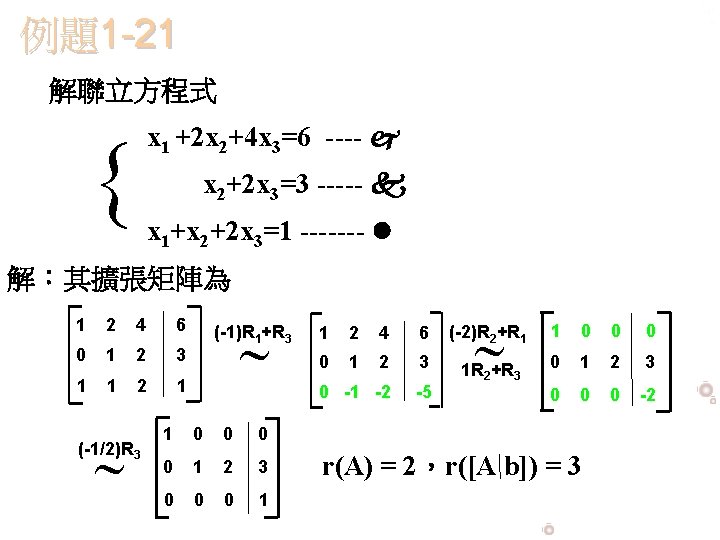
Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download
連立方程式 例題
連立方程式 例題-例題12 家から学校 までそれぞれ何分歩きましたか. (1) 家から橋まで x 分,橋から学校まで y 分歩いたとして連立方程式 を作ると, (距離)は(速さ)×(時間)で求めます. 50x80y=10 (1) ←距離の関係から xy=15 (2) ←時間の関係から (2) 家から橋まで,橋から学校までそれぞれ何分 10倍、100倍して小数を消せばいいよ! というわけで、今回の記事では「小数を含む連立方程式の解き方」についてイチから解説していきます。 今回の記事では以下の問題の解き方について解説していくぞ! 次の計算をしなさい。 ① ② ③ 方程式の基本




世界一わかりやすい数学問題集中2 2章 連立方程式
うまく解けない場合もある 解がたくさん出てくる ; 連立微分方程式の解法 先に学んだ微分演算子法やラプラス変換により、連立微分方程式を解くことができる。 その例を見てみよう。以下では、\(x=x(t)、y=y(t)\)とする。 微分演算子による行列式と連立1次方程式 例題集 Q 1 クラメルの公式を使って, 次の連立 1 次方程式を解きなさい。 { 5 x 4 y 3 z = 7 − 4 x 3 y − 2 z = − 1 − 3 x − 2 y − 3 z = 1 解答・解説を見る
== 連立方程式の作り方・・・文章題 == 例題1 りんご1個の価格がみかん2個の価格よりも50円高く,みかん3個の価格よりも30円安いものとする. みかん1個の価格を x (円),りんご1個の価格を y (円)とすると, x , y が満たす連立方程式は< 制御と振動の数学 第一類 連立微分方程式の解法 例題による考察 ナビゲーションに移動 検索に移動 例104 {\displaystyle \quad }11 1 階線形・定数係数・同次型 定数係数の同次型連立微分方程式y′ = Ay の解法を考える。 通常の(非連立)1階線形微分方程式からの類推に より、この方程式の解がy = Ce xv のような形であると仮定してみよう。 ここで、Cは定数、v はxによらない定 数ベクトルである。
連立方程式の文章問題 道のり・速さ・時間についての練習問題です。 解説記事はこちら gt;連立方程式の利用(文章問題)解き方まとめ スポンサーリンク 目次1 方程式練習問題連立方程式の文章問題~道のり・速さ・時間① と ③ を連立方程式として解くと ,\ これらは問題に適している。 p % の食塩水 j, % の食塩水 j 13 説 昨年の入学者のうち,男子を 人,女子を \ 人とすると \ \ よって 連立一次方程式の解法 連立一次方程式の解法 < Back to the video list search Search inside video Tweet Slides Related classes/ C Programming Kikan(1) Subject teacher: SAITO, Daisuke C Programming Kikan(2) Subject teacher: GOTO, Yuichi/YOSHIOKA, Tsuyoshi more How to use this site About Waseda Course Channel;




3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく



1 3 2 1 4 2 2 15r
Page Top >About copyright / >Policy on 連立合同式・中国剰余定理の本質的な部分を理解するために,このページでは二元の場合で n 1, n 2 n_1, n_2 n 1 , n 2 が互いに素な場合のみを考えます。より一般の場合は→中国剰余定理と法が互いに素でない場合への拡張 目次 連立合同式の簡単な例題 中国剰余定理の証明(解の唯一性)A n1 a n2 a n3!



連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料




連立方程式 代入法 計算ドリル 問題集 数学fun
Dlnx = Adt ¡!この連立方程式では,(1)(2)の y の係数の符号だけが逆の同じ係数になっているので,(1)(2)の各辺を「足し算」すると y を消去できます. (答案) (1)(2) 3x−4y=7 ) 5x4y=33 8x ___ =40 x=5 これを(1)に代入すると 3 × 5−4y=7 _____ −4y=−8 _____ y=2 よって連立方程式の解は連立 次方程式の基礎知識 ~および の消去法の安定性について~ 渡部善隆 学会や研究集会での発表や、そこでの議論を聞いていると、 時間が限られていることもあって ある「知識」を持っていることが前提となって話が進んでいく場合がよくあります。特に数値計算の 分野では、「××




中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




國二junior High数学的連立方程式の文章題筆記 Clear
第12章「微分方程式」の問題 例題12-1 dy dx = −xy2 を解け (例題12-1の解答)変数分離形であるので変形して両辺を積分する と, Z − 1 y2 dy = Z xdx y = 2 x2 C (C は積分定数) 類題12-1 以下の変数分離型微分方程式を解きなさい (1) dy dx = exy (2) dy dx = xy (3) dy dx 連立一次方程式①(掃き出し法) 例題を解きながら掃き出し法を用いて連立一次方程式を解く方法をコツとともにわかりやすく解説します。 解き方 掃き出し法は、拡大係数行列の簡約化をすることと一緒である。 定価・原価・利益の問題(連立方程式) 問題文の中に、求める数が2つある場合は、それぞれを 、 で表します。 ただし、問題によっては、求める数に関連のある数を 、 としたほうが解きやすい場合もあります。 問題文から等しい関係にあるものを見つけ出し、2つの方程式をつくります。 商品を売るときには、原価(仕入れ値)にいくらかの利益を見込ん



1 3 2 1 4 2 2 15r




單元8 三元一次聯立方程式例題2 動態解題 Youtube
連立方程式(計算練習1) 連立方程式を解け x=2y5 x3y=7 x3y=7 x5y=11 2x3y=8 x5y=11 x2y=4 x3y=7 x2y=10 x=3y5 2x5y=11 3x4y=6 xy=10 x=y4 01x05y=13 03x04y=06 3xy=5 2(x3y)=14 2 3 x 1 5 y= 8 15 2 5 x 3 10 y= 2 5 1 2 x 2 3 y= 1 6 3 2 x 7 6 y= 13 6 x3y=4x6y=2これを行列表示すると、 A= a 11 a 12 a 13!連立方程式の計算は、行列の考え方を利用することで解くことができる。 上記のような連立方程式は以下のように 行列で記述することができる。 とおくと、求めたい 1, 2, 3は 以下のように求めることができる。 連立方程式の計算 28




ちょっと複雑な連立方程式を練習しよう インターネット家庭教師のアスミラ




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook
連立微分方程式をベクトル形式であらわすと dx dt = Ax (19) という形になることをみました。この形を見て 1 x dx = Adt ¡!連立方程式 例題 連立方程式 (代入法) 連立方程式 (加減法1) 連立方程式 (加減法2) 連立方程式 (かっこのある式) 連立方程式 (A=B=C) 連立方程式 解と係数 連立方程式 解と係数2 文章題 代金と個数 文章題 代金と個数2 文章題 速さ1 文章題 速さ2 文章題 速さ3 文章題速さ 往復 文章題速さ 出会う追いつく 文章題速さ 長さのあるもの 文章題 2けたの自然数 文章題 商と余り例題1次の連立方程式を解きなさい。$\left\{ \begin{array}{@{}1} 06x12y=3\\ 2x08y=04 \end{array} \right $解説\(1\) 次方程式を解くときと同じです。等式の両辺を \(10\) 倍、\(100\) 倍して小数点がない式にしてしまいましょう。$\left\{ \begin{array}{@{}1} 06x12y=3 ・・・①\\ 2x08y=04 ・ 中学数学の基本から難問まで




例題 解聯立方程式 高中的數學 Math Pro 數學補給站



第1章 連立方程式
文章題をとおして、連立方程式を具体的な場面で活用し、解く練習をする問題プリントです。 連立方程式の活用 練習問題 (1) 答えガウスの消去法(定理22 変形定理) 本項目の目的 ;連立方程式(代入法のやさしい問題) 例題1 次の連立方程式を解いてください. (1) (2) 2つの文字 が含まれている連立方程式を解くには,加減法や代入法を使って,どちらか一方の文字を消去し,1つの文字だけの方程式に直して解くようにします. この問題のように の形の式があると ,代入によって を消去することができます. 解き方の流れ




27 二元一次聯立方程式的分配問題例題 Youtube



1
連立方程式 例題 連立方程式 (代入法) 連立方程式 (加減法1) 連立方程式 (加減法2) 連立方程式 (かっこのある式) 連立方程式 (A=B=C) 連立方程式 解と係数 連立方程式 解と係数2 文章題 代金と個数 文章題 代金と個数2 文章題 速さ1 文章題 速さ2 文章題 速さ3 文章題速さ 往復 文章題速さ 出会う追いつく 文章題速さ 長さのあるもの 文章題 2けたの自然数 文章題 商と余り定数係数連立線形常微分方程式— 11 同次方程式 y = 0 B B B B B B @ y1 y2 yn 1 C C C C C C A, A = 0 B B B B B B @ a1,1 a1,2 ··a1,n a2,1 a2,2 ··a2,n an,1 an,2 ··an,n 1 C C C C C C A とおいて、同次方程式(1) を次の様に書く: dy dt = Ay (2) 定義 方程式 の 個の解 に対し行列2年生 2 連立方程式 知識・技能の習得を図る問題 年 組 号氏名 練習問題① 1 解が(x ,y )=(-1,4)になる連立二元一次方程式を1つつくりなさい。 2 解が(x ,y )=(2,1)になる連立方程式を次のアからオの中からすべて選びなさい。 ア 2x +y =1 イ 3x +4y =10 ウ 2x -3y =7




中2数学 カッコ 分数を含む連立方程式 例題編 映像授業のtry It トライイット




中2数学 1次関数と連立方程式 例題編 映像授業のtry It トライイット
掃き出し法を用いた連立1次方程式の解法と例題 線形代数 ライター: y0he1 当ページでは、掃き出し方を使って連立1次方程式の解を求める方法や実際に連立1次方程式の解を求める手順を各ステップごとに丁寧に解説しています。 クラメルの公式で解くA 1n a 21 a 22 a 23!2つの文字 が含まれている連立方程式を解くには,加減法や代入法を使って,どちらか一方の文字を消去し,1つの文字だけの方程式に直して解くようにします. この問題のように の係数がそろっているときは,左辺どうし,右辺どうしを引くと を消去することができます.




世界一わかりやすい数学問題集中2 2章 連立方程式




例題 代入消去法 Y Ax B 數學 均一教育平台
(3)作った連立方程式を、もっとも簡単な解き方・方法で解く (4)求めた連立方程式の解が答えとしてふさわしいかどうかを確認して、単位をつけて答えを書く 2、平均の問題(応用) 例題1:ある中学校の生徒80人が学力テストを受験した。全体の平均点は58点で、男子の平均点は52点、女子の平均点は62点であった。男子・女子の人数はそれぞれ何人か。連立一次方程式の解を求める方法には、掃き出し法があった。 逆行列① (簡約化) 例題を解きながら逆行列を簡約化を用いて求める方法をコツを交えながらわかりやすく解説します。 逆行列は行列の逆数に相当する概念であり、定義とその求め方の両方を理解しておくことが大切です。 一方、掃き出し法よりも逆行列を用いる方法が有効な場合がある。 の係数連立方程式(加減法1)_ 例題と練習 連立方程式(加減法2)_ 例題と練習 連立方程式(代入法1) 連立方程式(代入法2) 連立方程式(加減法1) 連立方程式(加減法2) 連立方程式(加減法3) 連立方程式(加減法4) 連立方程式(分数1) 連立方程式(分数2) 連立方程式(分数3) 連立方程式(分数4) 連立方程式(分数5) 連立方程式(分数6) 連立方程式(分数7) 連立方程式(分数8) 連立方程式(分数9) 連立方程




連立方程式の解き方と交点の座標の求め方 数学の偏差値を上げて合格を目指す




中2数学 連立方程式の文章題 割合 例題編 映像授業のtry It トライイット
A nn " # $ $ $ $ $ $ $ % & ' ' ' ' ' ' ' ⋅ = ⋅ x n x x x 2 1 ⋅ = ⋅ b n b b b 1 Ax =b 1 クラメールの公式 A が正則(det A ≠0連立方程式 例題 連立方程式(代入法) 連立方程式(加減法1) 連立方程式(加減法2) 連立方程式(かっこのある式) 連立方程式(a=b=c) 連立方程式 解と係数 連立方程式 解と係数2 文章題 代金と個数 文章題 代金と個数2 文章題 速さ1 文章題 速さ2 文章題 速さ3 文章題速さ 往復 文章題速さ 出会う追いつく 文章題速さ 長さのあるもの 文章題 2けたの自然数 文章題 商と余り 文章題X = x(0)eAt (110) と"解"が求まるんじゃないのと洞察された方は凄い!ただ解に含まれるeAt という,指数関数の肩に行列Aが 乗っているものをどう処理するかという




三元一次方程组练习题 三元一次聯立方程式題目



50 連立方程式例題 犬イラスト
当ページでは連立1次方程式を、クラメルの公式を用いて、解く方法をご紹介いたします。 掃き出し法を使って連立一次方程式を解く方法に関してはこちらで紹介しております。 クラメルの公式 公式 \(\begin{eqnarray} \left\{ \begin{array}{l} a_{11}x_1 a_{12}x_2連立方程式 例題 連立方程式 (代入法) 連立方程式 (加減法1) 連立方程式 (加減法2) 連立方程式 (かっこのある式) 連立方程式 (A=B=C) 連立方程式 解と係数 連立方程式 解と係数2 文章題 代金と個数 文章題 代金と個数2 文章題 速さ1 文章題 速さ2 文章題 速さ3 文章題速さ 往復 文章題速さ 出会う追いつく 文章題速さ 長さのあるもの 文章題 2けたの自然数 文章題 商と余り 方程式の解き方が分かっていれば、すんなり内容が入ってくると思います。 それでは、例題を使って理解していきましょう! *第1回:院試対策線形代数①(同次連立1次方程式)




3分でわかる 連立方程式の代入法と加減法をわかりやすく 合格サプリ




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
連立一次方程式 n 個の変数を含む以下のn 元連立一次方程式の解法を考える。 !



中2第2章29連立方程式の利用 解と連立方程式




例題10 解含分數的二元一次聯立方程式 Youtube



Q Tbn And9gcsm6 Ygdifx7pydebyfkxkcficln0q2usbh7vlhkbagbczf8kws Usqp Cau



中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




1 3 2 1 4 2 2 15r




50 連立方程式例題 犬イラスト




連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学



秋篠理数 算数教室の さあさあ お勉強だよ




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




1 3 2 1 4 2 2 15r




中2数学 連立方程式の文章題 基礎 例題編 映像授業のtry It トライイット




例題 克拉瑪公式解二元一次方程組 Youtube




トップ100連立方程式公式 最高のカラーリングのアイデア




15 加減消去法解二元一次聯立方程式例題 Youtube




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook




像上面兩個二元一次方程式x Y 70 和x 2y 115 雖然各自有解 但是當聯立在一起時 我們要找的就是同時能讓兩個方程式等號成立的x Y 值 此時的x 與y 就是這兩個方程式的一組共同解 也就是聯立方程式的解 但是 要如何求出二元一次聯立方程式的解呢 讓我們先以二




トップ100連立方程式公式 最高のカラーリングのアイデア




連立3元1次方程式 まなびの学園




例題付き 連立方程式の解き方と失敗しないコツ




均一影片 例題 解二元一次聯立方程式 綜合應用1 學習單 Shareclass




例題 解二元一次聯立方程式 綜合應用1 數學 均一教育平台




Chapter 2 聯立線性方程式與矩陣緒言線性方程式組 Systems Of Linear Equations 出現在多數線性模式 Linear Model 中 根據以往解題的經驗 讀者們也許已發現方程式的解僅與該方程式的係數有關 求解的過程也僅與係數的運算有關 只要係數間的相關位置不改變 Ppt



例 二元一次方程組及其解 台灣數位學苑 K12 數學




例題付き 連立方程式の解き方と失敗しないコツ



Q Tbn And9gctsdhxnqxebsyoonhfly Qastncurd5xayp0punpcetuujdufxx Usqp Cau



1 3 2 1 4 2 2 15r




うさぎでもわかる微分方程式 Part10 連立微分方程式 2階微分方程式に帰着させて解くパターン 工業大学生ももやまのうさぎ塾



連立方程式とは 代入法と加減法 計算問題や文章題の解き方 受験辞典




二元一次聯立方程式的基礎概念 數學 均一教育平台




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




高校入試 解き方 が身につく問題集 数学 Amazon Com Books




中2数学 1次関数と連立方程式 例題編 映像授業のtry It トライイット
.png)



2元一次方程式題目初中數學 二元一次方程式 例題2 Gquhm



1




例題付き 連立方程式の解き方と失敗しないコツ
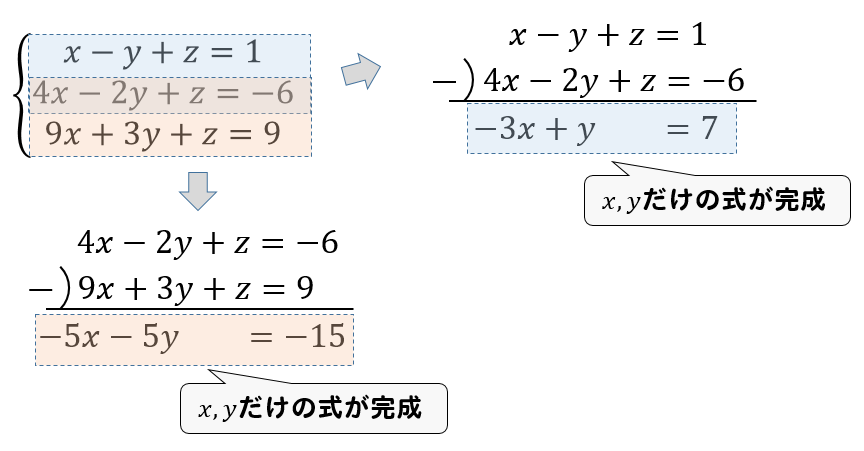



連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト




例題付き 連立方程式の解き方と失敗しないコツ



課程介紹 二元一次聯立方程式 發現學習的美麗新世界




連立方程式 問題 Youtube




第9 章線性微分方程組 Ppt Download



連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料




1 3例題2三元一次聯立方程式的無解 Youtube




中学数学 連立方程式 加減法 中学数学の無料オンライン学習サイトchu Su
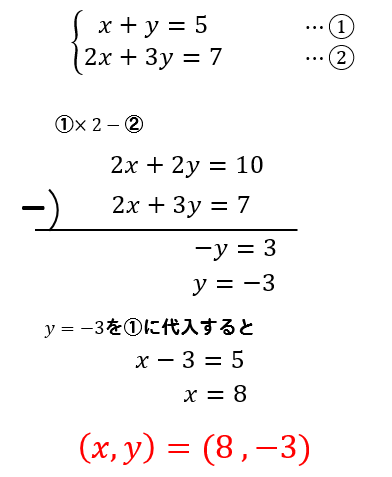



方程式練習問題 連立方程式 A B C 方程式の解き方まとめサイト




例題1 求聯立方程式的解 Youtube



50 連立方程式例題 犬イラスト
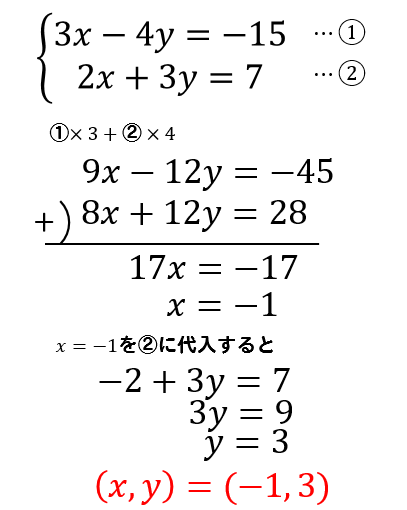



連立方程式 加減法の解き方をわかりやすく問題を使って徹底解説 数スタ




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




世界一わかりやすい数学問題集中2 2章 連立方程式




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




無料ダウンロード中1 方程式文章問題 最高のカラーリングのアイデア




無料ダウンロード中1 方程式文章問題 最高のカラーリングのアイデア



コンピュータ機械工学




例題 解二元一次聯立方程式 綜合應用1 數學 均一教育平台



Math 超簡単 連立方程式の利用 働きアリ The 2nd




連立方程式の2つの解き方 代入法 加減法 数学fun




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook




例題付き 連立方程式の解き方と失敗しないコツ




2 二元三次方程式
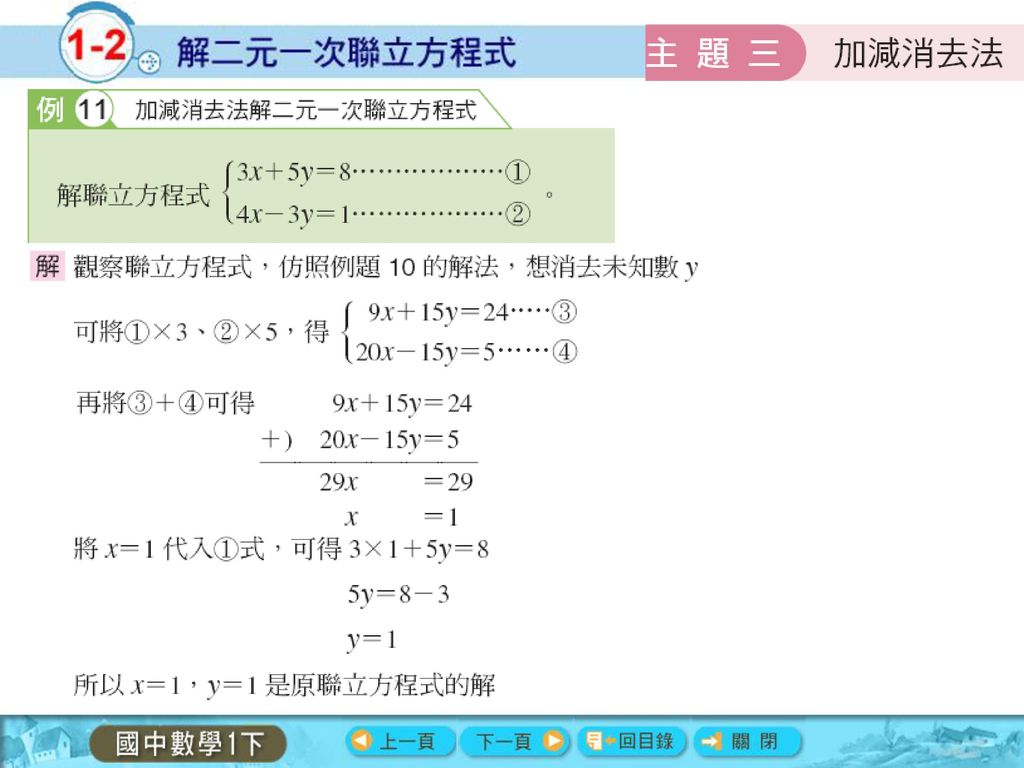



像上面兩個二元一次方程式x Y 70 和x 2y 115 雖然各自有解 但是當聯立在一起時 我們要找的就是同時能讓兩個方程式等號成立的x Y 值 此時的x 與y 就是這兩個方程式的一組共同解 也就是聯立方程式的解 但是 要如何求出二元一次聯立方程式的解呢 讓我們先以二




东京大学工学系研究科数学套路总结系列 常微分方程式过去问应用型 华为云




トップ100連立方程式公式 最高のカラーリングのアイデア




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




連立一次方程式を掃き出し法で解く6つの例題 理数アラカルト




1 2 解二元一次聯立方程式主題一 二元一次聯立方程式主題二 代入消去法主題三 加減消去法重點整理新竹縣立湖口國民中學
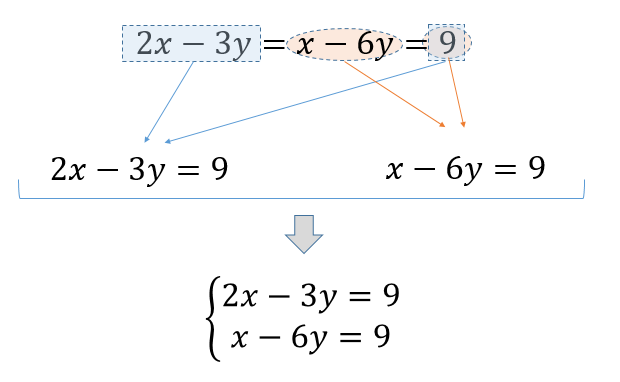



連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト



第1章 連立方程式




17 調整係數解二元一次聯立方程式 1 例題 Youtube




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook




均一影片 例題 解二元一次聯立方程式 綜合應用3 學習單 Shareclass
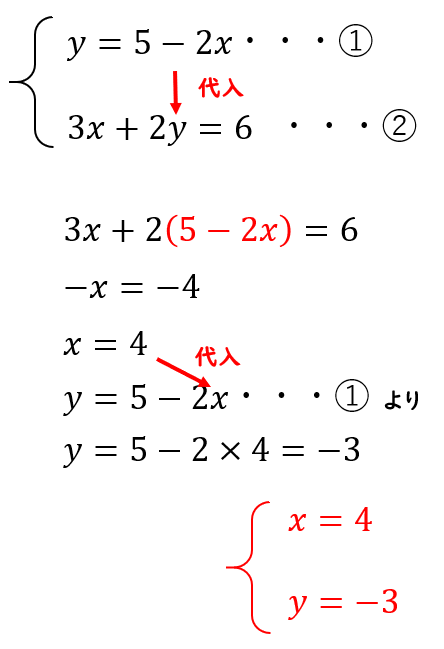



連立方程式の2つの解き方 代入法 加減法 数学fun




高校数学で学習する連立方程式の解き方まとめ 数スタ




世界一わかりやすい数学問題集中2 2章 連立方程式




連立方程式の解き方 の問題のわからないを5分で解決 映像授業のtry It トライイット



第1章 連立方程式




連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト




例題 解二元一次聯立方程式 綜合應用3 數學 均一教育平台



一個數學題目 三元三次方程式求解 三元三次方程式




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook




鉄則10 方程式 連立方程式 一般 寺田の数学合格鉄則96に関するメモ



0 件のコメント:
コメントを投稿